多智能体强化学习 (Multi-Agent Reinforcement Learning, MARL)
前置知识:深度强化学习算法一图流
1 多智能体强化学习的 4 中情境
1.1 完全合作关系 (Fully Cooperative)
所有的 Agent 具有共同的目标。
例:多个汽车组装机器人协作组装汽车。
1.2 完全竞争关系 (Fully Competitive)
一方的收益是另一方的损失。
例:零和博弈。
1.3 合作与竞争混合关系 (Mixed Cooperative & Competitive)
例:机器人足球比赛。两支球队之间是竞争关系,球队内部的机器人之间是合作关系。
1.4 利己主义 (Self-Interested)
每个 Agent 仅最大化自身利益,不考虑其他 Agent 是否获利或损失。
例:股票交易系统。
2 多智能体强化学习术语
2.1 基本概念
假设系统中存在 $n$ 个 Agent
- 环境状态:$\textcolor{green}{S}$
- 第 $i$ 个 Agent 的动作:$\textcolor{red}{A^i}$
- 状态转移函数: $p(\textcolor{green}{s^\prime} | \textcolor{green}{s}, \textcolor{red}{a^1}, \textcolor{red}{\cdots}, \textcolor{red}{a^n}) = P(\textcolor{green}{S^\prime = s^\prime} | \textcolor{green}{S = s}, \textcolor{red}{A^1 = a^1}, \textcolor{red}{\cdots}, \textcolor{red}{A^n = a^n})$
- 第 $i$ 个 Agent 的奖励:$\textcolor{blue}{R^i}$
- Fully Cooperative: $\textcolor{blue}{R^1} = \textcolor{blue}{R^2} = \cdots = \textcolor{blue}{R^n}$ 在合作的情境下,所有 Agent 的奖励是相同的
- Fully Competitive: $\textcolor{blue}{R^1} \propto -\textcolor{blue}{R^2}$ 在竞争的情境下,一个 Agent 的奖励是另一个 Agent 的损失
- 第 $i$ 个 Agent 在 $t$ 时刻的回报:$U_t^i = \textcolor{blue}{R_{t}^i} + \textcolor{blue}{R_{t+1}^i} + \textcolor{blue}{R_{t+2}^i} + \textcolor{blue}{R_{t+3}^i} + \cdots$
- 折扣回报:$U_t^i = \textcolor{blue}{R_{t}^i} + \gamma \cdot \textcolor{blue}{R_{t+1}^i} + \gamma^2 \cdot \textcolor{blue}{R_{t+2}^i} + \gamma^3 \cdot \textcolor{blue}{R_{t+3}^i} + \cdots$
- 折扣率:$\gamma \in [0, 1]$
注 1:MARL 中下一个状态受所有 Agent 动作的影响。这意味着每个 Agent 都能够影响下一个状态,从而影响其他 Agent 。这说明 Agent 之间会相互影响,而非相互独立的。
注 2:单个 Agent 的奖励不仅与自己的动作有关,还与其他 Agent 的动作有关。(在足球比赛中,对方进的乌龙球可以增加我方的奖励)
- 第 $i$ 个 Agent 的策略网络: $\pi(\textcolor{red}{a^i} | \textcolor{green}{s}; \theta^i)$
- 有些场景的 Agent 可以使用相同的策略网络 $\theta^1 = \theta^2 = \cdots = \theta^n$(自动驾驶汽车可以使用相同的策略)
- 有些场景的 Agent 需要使用不同的策略网络 $\theta^i \neq \theta^j$(球队中担任不同职责的球员)
2.2 回报的随机性来源分析
在当前时刻 $t$ ,第 $i$ 个 Agent 获得的奖励 $\textcolor{blue}{R_t^i}$ 与当前的状态 $\textcolor{green}{S_t}$ 和所有 Agent 的动作 $\textcolor{red}{A_t^1}, \textcolor{red}{A_t^2}, \cdots, \textcolor{red}{A_t^n}$ 有关。
那么在当前时刻 $t$ ,第 $i$ 个 Agent 的折扣回报 $U_t^i = \sum_{k=0}^{\infty}\gamma^k \cdot \textcolor{blue}{R_{t+k}^i}$ 依赖于:
- 当前时刻及其之后的所有状态 ${\textcolor{green}{S_t}, \textcolor{green}{S_{t+1}}, \textcolor{green}{S_{t+2}}, \cdots}$
- 所有 Agent 当前时刻及其之后的所有动作 ${\textcolor{red}{A_{t}^j}, \textcolor{red}{A_{t+1}^j}, \textcolor{red}{A_{t+2}^j}, \cdots}$,其中 $j = 1, 2, \cdots, n$
2.3 状态价值函数
第 $i$ 个 Agent 的状态价值函数: $V^i(\textcolor{green}{s_t}; \theta^1, \theta^2, \cdots, \theta^n) = \mathbb{E}[U_t^i | \textcolor{green}{S_t = s_t}]$
- 对 $t+1$ 时刻及之后的所有状态 ${\textcolor{green}{S_{t+1}}, \textcolor{green}{S_{t+2}}, \cdots}$ 求期望
- 对 $t$ 时刻及之后的所有 Agent 的所有动作 ${\textcolor{red}{A_{t}^j}, \textcolor{red}{A_{t+1}^j}, \textcolor{red}{A_{t+1}^j}, \cdots}, (j = 1, 2, \cdots, n)$ 求期望
- 即:对除 $\textcolor{green}{S_t}$ 以外的所有状态和动作求期望
注:所有 Agent 的动作服从各自的策略分布 $\textcolor{red}{A_t^j} \sim \pi(\textcolor{red}{\cdot} | \textcolor{green}{s_t}; \theta^j), (j = 1, 2, \cdots, n)$ 。因此动作的期望与策略网络有关。这就是为什么第 $i$ 个 Agent 的状态价值函数与所有 Agent 的策略网络有关。
解释:如果你的队友 $\theta^j$ 很菜,那么你自己也无法获得很高的奖励,所以你的状态价值函数 $V^i$ 就会较小。如果你的队友 $\theta^j$ 很强,那么你自己也能获得很高的奖励,所以你的状态价值函数 $V^i$ 就会较大。
如果其中一个 Agent 改变了策略,那么所有 Agent 的状态价值函数都会发生变化。
例:如果球队中一个前锋改进了策略,那么他的队友的状态价值函数就会变大,而对手的状态价值函数就会变小。
3 多智能体强化学习的收敛问题
单智能体强化学习的目标是最大化状态价值函数的期望: \(\max_{\theta} J(\theta) = \mathbb{E}_{\textcolor{green}{S}}[V(\textcolor{green}{S}; \theta)]\) 随着策略网络 $\theta$ 的更新,当 $J(\theta)$ 不再变大时,我们认为策略网络 $\theta$ 已经收敛。
判断多智能体强化学习的标准是 是否达到纳什均衡 (Nash Equilibrium) 。
纳什均衡:在其他 Agent 都不改变策略的情况下,一个 Agent 无论怎样改变策略都无法让自己获得更高的回报。
不能使用单智能体的训练方法训练多智能体
如果使用单智能体的训练方法,那么第 $i$ 个 Agent 的状态价值函数为: \(V^i(\textcolor{green}{s_t}; \theta^1, \theta^2, \cdots, \theta^n)\) 其训练目标为最大化状态价值函数的期望: \(J^i(\theta^1, \theta^2, \cdots, \theta^n) = \mathbb{E}_{\textcolor{green}{S}}[V^i(\textcolor{green}{S}; \theta^1, \theta^2, \cdots, \theta^n)]\) 即: \(\max_{\theta^i} J^i(\theta^1, \theta^2, \cdots, \theta^n)\)
每一个 Agent 都在最大化各自的目标函数:
| Agent | 优化目标 |
|---|---|
| Agent $\textcolor{purple}{1}$ | $\max_{\textcolor{purple}{\theta^1}} J^{\textcolor{purple}{1}}(\textcolor{purple}{\theta^1}, \theta^2, \cdots, \theta^n)$ |
| Agent $\textcolor{purple}{2}$ | $\max_{\textcolor{purple}{\theta^2}} J^{\textcolor{purple}{2}}(\theta^1, \textcolor{purple}{\theta^2}, \cdots, \theta^n)$ |
| $\cdots$ | $\cdots$ |
| Agent $\textcolor{purple}{n}$ | $\max_{\textcolor{purple}{\theta^n}} J^{\textcolor{purple}{n}}(\theta^1, \theta^2, \cdots, \textcolor{purple}{\theta^n})$ |
如果第 $i$ 个 Agent 已经找到了最优策略 $\theta_{\star}^i = \arg\max_{\theta^i} J^i(\theta^1, \theta^2, \cdots, \theta^n)$ ,那么当其他 Agent 改进策略 $\theta^j$ 时,第 $i$ 个 Agent 的目标函数 $J^i$ 就会发生变化,原本的最优策略 $\theta_{\star}^i$ 就不再是最优策略。因此第 $i$ 个 Agent 就需要重新寻找最优策略。所有的 Agent 都在寻找最优策略的过程中不断地改变策略,这会导致所有 Agent 的目标函数一直在变化,从而导致多智能体的训练无法收敛。
4 多智能体强化学习训练方法
多智能体强化学习的训练方式主要包括三种:去中心化 (Fully Decentralized)、完全中心化 (Fully Centralized) 和中心化训练去中心化执行 (Centralized Training with Decentralized Execution)。
本章首先引出 MARL 中涉及到的不完全观测 (Partial Observation) 概念,然后分别介绍上述三种训练方法。
4.1 不完全观测 (Partial Observation)
在多智能体系统中,每个 Agent 往往只能观测到环境状态 $\textcolor{green}{s}$ 的一部分。
将第 $i$ 个 Agent 观测到的状态记为 $\textcolor{green}{o^i}$
- 对于完全观测 (Fully Observation) :$\textcolor{green}{o^1} = \textcolor{green}{o^2} = \cdots = \textcolor{green}{o^n} = \textcolor{green}{s}$
- 对于不完全观测 (Partial Observation) :$\textcolor{green}{o^i} \neq \textcolor{green}{s}$ (不同 Agent 通常有不同的局部观测)
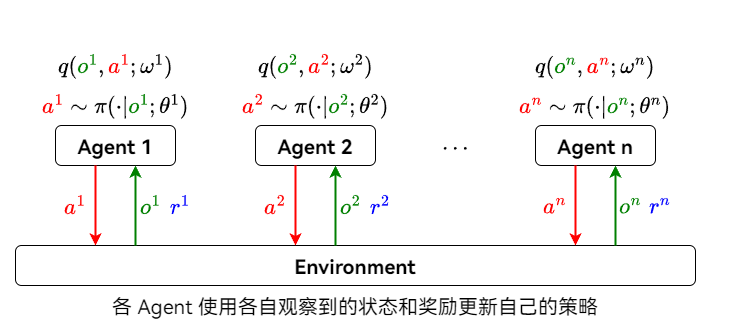
4.2 去中心化 (Fully Decentralized) 架构
每个 Agent 独立与环境交互,仅使用自己的观测和奖励来更新自己的策略。Agent 之间不交换信息。
去中心化架构的本质是单智能体强化学习。在上一章中说明了去中心化训练存在的问题。
Fully Decentralized Actor-Critic Method
- 第 $i$ 个 Agent 拥有独立的策略网络 (Actor) : $\pi(\textcolor{red}{a^i} | \textcolor{green}{o^i}; \theta^i)$
- 第 $i$ 个 Agent 拥有独立的价值网络 (Critic) : $q(\textcolor{green}{o^i}, \textcolor{red}{a^i}; \omega^i)$
- Agent 之间不交换观测、动作和奖励信息
- 策略网络和价值网络的训练方式与单智能体强化学习相同
- 使用策略梯度更新 $\theta^i$
- 使用 TD 算法更新 $\omega^i$
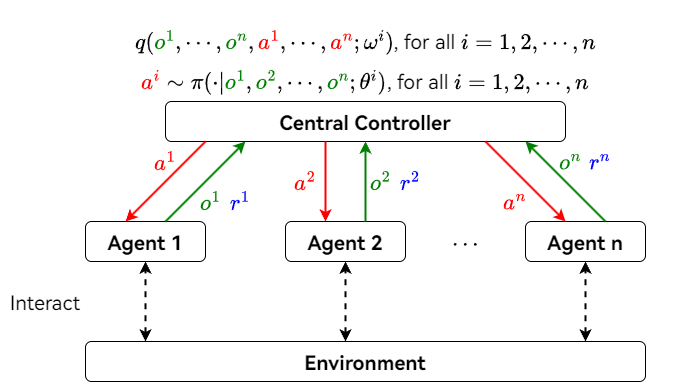
4.3 完全中心化 (Fully Centralized) 架构
所有 Agent 将观测状态和奖励发送给中央控制器 (Central Controller) ,中央控制器根据所有 Agent 的动作、观测和奖励来更新所有 Agent 的策略。并且由中央控制器负责所有 Agent 的决策。Agent 只负责执行动作,不进行决策。
Fully Centralized Actor-Critic Method
- 所有 Agent 的观测向量记为 $\textcolor{green}{\pmb{o} = [o^1, o^2, \cdots, o^n]}$
- 所有 Agent 的动作向量记为 $\textcolor{red}{\pmb{a} = [a^1, a^2, \cdots, a^n]}$
- 中央控制器知晓 $\textcolor{green}{\pmb{o}}$、$\textcolor{red}{\pmb{a}}$ 和所有 Agent 的奖励
- 中央控制器拥有所有 Agent 的策略网络 $\pi(\textcolor{red}{a^i} | \textcolor{green}{\pmb{o}}; \theta^i)$ ,其中 $i = 1, 2, \cdots, n$
- 接受所有 Agent 的观测 $\textcolor{green}{\pmb{o}}$,输出第 $i$ 个 Agent 动作的分布
- 中央控制器拥有所有 Agent 的价值网络 $q(\textcolor{green}{\pmb{o}}, \textcolor{red}{\pmb{a}}; \omega^i)$,其中 $i = 1, 2, \cdots, n$
- 根据所有 Agent 的观测和动作进行评分
- 训练
- 中央控制器接收所有 Agent 的观测、动作和奖励
- 使用策略梯度更新所有 Agent 的策略网络 $\theta^i$
- 使用 TD 算法更新所有 Agent 的价值网络 $\omega^i$
- 执行
- 所有 Agent 将其观测 $\textcolor{green}{o^i}$ 发送给中央控制器
- 中央控制器根据所有 Agent 的观测 $\textcolor{green}{\pmb{o} = [o^1, o^2, \cdots, o^n]}$ 随机抽样所有 Agent 的动作 $\textcolor{red}{a^i} \sim \pi(\textcolor{red}{\cdot} | \textcolor{green}{\pmb{o}}; \theta^i)$
- 中央控制器将所有动作 $\textcolor{red}{a^i}$ 下发给对应的 Agent 执行
缺点
在中央控制器决策时,需要等待所有 Agent 将观测发送给中央控制器。因此中央控制器只有在收到所有 Agent 的观测后才能下发动作,从而增加了执行动作的延迟。
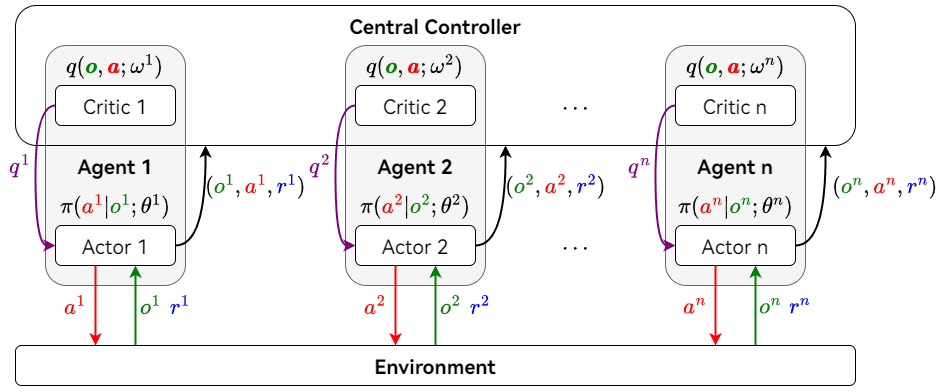
4.4 中心化训练去中心化执行 (Centralized Training with Decentralized Execution)
每个 Agent 拥有自己的策略网络。中央控制器收集所有 Agent 的观测、动作和奖励,辅助每个 Agent 训练自己的策略网络。训练结束后,中央控制器不再参与决策,每个 Agent 根据自己的策略网络执行动作。
Centralized Training with Decentralized Execution Actor-Critic Method
参考文献:
Multi-agent actor-critic for mixed cooperative-competitive environments.
Counterfactual multi-agent policy gradients.注:此处的架构与参考文献相比进行了简化,因此与文中的架构有所不同。
- 所有 Agent 的观测向量记为 $\textcolor{green}{\pmb{o} = [o^1, o^2, \cdots, o^n]}$
- 所有 Agent 的动作向量记为 $\textcolor{red}{\pmb{a} = [a^1, a^2, \cdots, a^n]}$
- 第 $i$ 个 Agent 拥有独立的策略网络 $\pi(\textcolor{red}{a^i} | \textcolor{green}{o^i}; \theta^i)$
- 中央控制器拥有所有 Agent 的价值网络 $q(\textcolor{green}{\pmb{o}}, \textcolor{red}{\pmb{a}}; \omega^i)$,其中 $i = 1, 2, \cdots, n$
- 训练
- 每个 Agent 根据自己的策略网络 (Actor) $\pi(\textcolor{red}{a^i} | \textcolor{green}{o^i}; \theta^i)$ 执行动作 $\textcolor{red}{a^i}$ ,并把动作、观测和奖励 $(\textcolor{green}{o^i}, \textcolor{red}{a^i}, \textcolor{blue}{r^i})$ 发送给中央控制器
- 中央控制器使用所有 Agent 上传的动作、观测和奖励 ${\textcolor{green}{o^i}, \textcolor{red}{a^i}, \textcolor{blue}{r^i}}_{i=1}^n$ 训练所有 Agent 的价值网络 (Critic) $q(\textcolor{green}{\pmb{o}}, \textcolor{red}{\pmb{a}}; \omega^i)$
- 使用 TD 算法更新价值网络参数 $\omega^i$
- 使用所有观测 $\textcolor{green}{\pmb{o} = [o^1, o^2, \cdots, o^n]}$
- 使用所有动作 $\textcolor{red}{\pmb{a} = [a^1, a^2, \cdots, a^n]}$
- 仅使用第 $i$ 个 Agent 的奖励 $\textcolor{blue}{r^i}$
- 中央控制器将 $\textcolor{purple}{q^i}$ 下发给每个 Agent 的 Actor
- 使用策略梯度更新策略网络参数 $\theta^i$
- 使用第 $i$ 个 Agent 的观测 $\textcolor{green}{o^i}$
- 使用第 $i$ 个 Agent 的动作 $\textcolor{red}{a^i}$
- 使用第 $i$ 个 Agent 的评分 $\textcolor{purple}{q^i}$
- 策略网络的更新不需要其他 Agent 的信息,因此可以在 Agent 本地进行训练
- 执行
- Agent 的执行过程不需要中央控制器参与
- 每个 Agent 使用自己的 Actor 独立与环境交互
5 神经网络共享参数问题
共享参数的策略:
- 所有 Agent 全部共享参数
- $\theta^1 = \theta^2 = \cdots = \theta^n$
- $\omega^1 = \omega^2 = \cdots = \omega^n$
- 部分 Agent 共享参数
- $\theta^i = \theta^j, (i \neq j)$
- $\omega^i = \omega^j, (i \neq j)$
- Agent 之间不共享参数
- $\theta^i \neq \theta^j$
- $\omega^i \neq \omega^j$
- 在足球机器人比赛中,机器人之间不应该共享参数,因为每个机器人的职责都不一样
- 无人驾驶汽车可以共享参数,因为每个汽车的任务都是一样的
6 总结
| 序号 | 架构 | Policy (Actor) | Value (Critic) |
|---|---|---|---|
| 1 | Fully Decentralized | $\pi(\textcolor{red}{a^i} | \textcolor{green}{o^i}; \theta^i)$ | $q(\textcolor{green}{o^i}, \textcolor{red}{a^i}; \omega^i)$ |
| 2 | Fully Centralized | $\pi(\textcolor{red}{a^i} | \textcolor{green}{\pmb{o}}; \theta^i)$ | $q(\textcolor{green}{\pmb{o}}, \textcolor{red}{\pmb{a}}; \omega^i)$ |
| 3 | Centralized Training Decentralized Execution | $\pi(\textcolor{red}{a^i} | \textcolor{green}{o^i}; \theta^i)$ | $q(\textcolor{green}{\pmb{o}}, \textcolor{red}{\pmb{a}}; \omega^i)$ |
- 第 1 种架构中,Agent 的策略网络和价值网络的输入均为本地信息,因此训练和执行都在本地进行
- 第 2 种架构中,Agent 的策略网络和价值网络的输入均为全局信息,因此训练和执行都在中央控制器进行
- 第 3 种架构中
- 策略网络与第 1 种架构相同,因此 Agent 可以去中心化执行
- 价值网络与第 2 种架构相同,因此 Agent 需要中心化训练